警告
本文最后更新于 2021-12-22,文中内容可能已过时。
![/images/img/008361837_1-177dbd1e09b007a92a3b401a61cb62f8.png]()
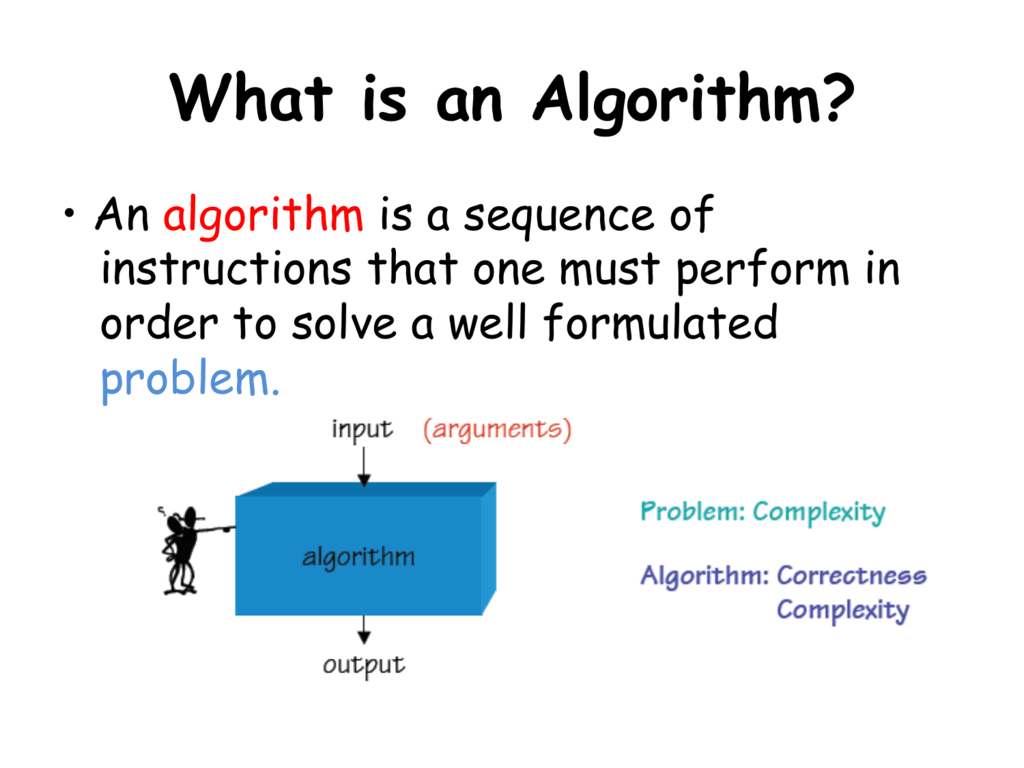
题目描述:
有N件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
输入格式:
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N行,每行两个整数 vi,wi用空格隔开,分别表示第 i件物品的体积和价值。
输出格式:
输出一个整数,表示最大价值
输入样例:
1
2
3
4
5
|
4 5
1 2
2 4
3 4
4 5
|
输出样例:
代码实现1
思路:
这类背包问题的特点是:每种物品仅有一件,可以选择放或不放。
子问题定义:f[i,v]表示前i件物品放入一个容量为v的背包中的得到的最大价值
状态转移方程为:
$$
f[i, v]=\max ({f[i-1, v],f[i-1, v-v_{i}]+w_{i})}
$$
考虑第i件物品放或者不放的问题,转化为只和前i-1物品相关的问题,如果第i件物品不放入背包,那总价值为$f[i-1, v]$;如果放第i件物品到背包中,也就是相当于把前i-1件物品放入容量为$v-v_{i}$的背包中,总价值为 $f\left[i-1, v-v_{i}\right]+w_{i}$.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include <iostream>
#include <cstring>
using namespace std;
int getMaxValue(int *w,int *v ,int N,int W)
{
int f[N+1][W+1];
memset(f,0,sizeof(f));
for(int i = 1;i <= N;i++)
{
for(int j = 0; j <= W; j++)
{
if (j >= w[i])
f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
else
f[i][j] = f[i - 1][j];
}
}
return f[N][W];
}
int main()
{
int N, W;
cin >> N >> W;
int w[N+1]{0};
int v[N+1]{0};
for (int i = 1; i <= N; i++)
{
cin >> w[i] >> v[i];
}
cout << getMaxValue(w,v,N,W) << endl;
return 0;
}
|
时间复杂度:$O(N*W)$
空间复杂度:$O(N*W)$
代码实现2(简化为1维DP)
子问题定义:f[j]表示N件物品,背包容量为j的背包中的得到的最大价值
状态转移方程为:
$$
f[j]=\max (f[j], f[j-v[i]]+w[i])
$$
注意:此时我们在更新f[j]的状态时需要逆序处理,避免前一轮的最优值被污染
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
#include <iostream>
#include <cstring>
using namespace std;
int getMaxValue(int *w,int *v ,int N,int W)
{
int f[W+1];
memset(f,0,sizeof(f));
for (int i = 1; i <= N; i++)
for (int j = W; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]); // 简化为1维DP
return f[W];
}
int main()
{
int N, W;
cin >> N >> W;
int w[N+1]{0};
int v[N+1]{0};
for (int i = 1; i <= N; i++)
cin >> v[i] >> w[i];
cout << getMaxValue(w,v,N,W) << endl;
return 0;
}
|
时间复杂度:$O(N*W)$
空间复杂度:$O(W)$
代码实现3(进一步减少额外存储空间)
将代码实现2中的代码进一步简化,不适用数组来存储每件物品的体积和价值而是采用临时变量存储,边输入边处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#include <iostream>
#include <cstring>
using namespace std;
const int MAX_N = 1010;
int f[MAX_N];
int main()
{
int N, W;
cin >> N >> W;
for (int i = 1; i <= N; i++)
{
int v,w; // 输入当前物品的体积和价值
cin >> v >> w; // 边输入边处理
for (int j = W; j >= v; j--)
f[j] = max(f[j], f[j - v] + w);
}
cout << f[W] << endl;
return 0;
}
|
时间复杂度:$O(N*W)$
空间复杂度:$O(W)$
题目描述:
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。
求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible.
给定一张边带权的无向图 G=(V,E),其中 V 表示图中点的集合,E 表示图中边的集合,顶点数为n=|V|,边数为m=|E|。
输入格式:
第一行包含两个整数 n和 m。
接下来 m行,每行包含三个整数 u,v,w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式:
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
注:不连通的图没有最小生成树
输入样例1:
1
2
3
4
5
6
|
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
|
输出样例1:
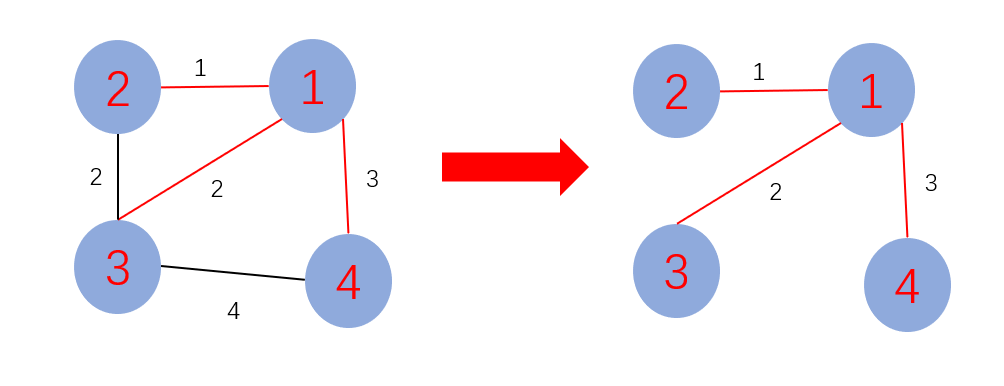
结果说明:
![/images/img/20211222135724.png /images/img/20211222135724.png]()
输出路径(构成最小成树的三条边):
输入样例2:
1
2
3
4
5
|
5 4
1 3 2
1 2 4
2 3 3
4 5 2
|
输出样例2:
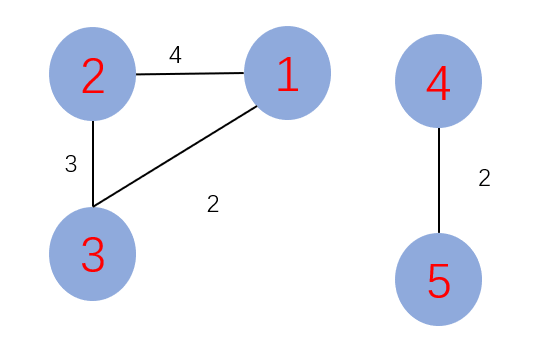
结果说明:
非连通图无法构成最小生成树!
![/images/img/20211222141114.png]()
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 510;
int g[N][N];//存储图
int dist[N];//存储各个节点到生成树的距离
int st[N];//节点是否被加入到生成树中
int pre[N];//节点的前驱节点
int n, m;//n 个节点,m 条边
const int INF = 0x3f3f3f3f; // 无穷大
int prim()
{
memset(dist,0x3f, sizeof(dist));//初始化距离数组为一个很大的数
int res= 0;
dist[1] = 0;//从 1 号节点开始生成
for(int i = 0; i < n; i++)//每次循环选出一个点加入到生成树
{
int t = -1;
for(int j = 1; j <= n; j++) //每个节点一次判断
{
if(!st[j] && (t == -1 || dist[j] < dist[t]))//如果没有在树中,且到树的距离最短,则选择该点
t = j;
}
if (i && dist[t] == INF) return INF; //无最小生成树
st[t] = 1; //选择该点
res += dist[t];
for(int i = 1; i <= n; i++)//更新生成树外的点到生成树的距离
{
if(dist[i] > g[t][i] && !st[i])//从t到节点i的距离小于原来距离,则更新。
{
dist[i] = g[t][i];//更新距离
pre[i] = t;//从t到i的距离更短,i的前驱变为 t.
}
}
}
return res;
}
void getPath()//输出各个边
{
for(int i = n; i > 1; i--)//n 个节点,所以生成树有n-1条边。
{
cout << i <<" " << pre[i] << " "<< endl;// i 是节点编号,pre[i] 是 i 节点的前驱节点。他们构成一条边。
}
}
int main()
{
memset(g, 0x3f, sizeof(g));//各个点之间的距离初始化成很大的数
cin >> n >> m;//输入节点数和边数
while(m --)
{
int a, b, w;
cin >> a >> b >> w;//输出边的两个顶点和权重
g[a][b] = g[b][a] = min(g[a][b],w);//存储权重
}
int ans = prim();
if (ans == INF) cout << "impossible" << endl;
else cout << ans << endl;//求最下生成树
//getPath();//去掉注释可以输出最小生成树的路径
return 0;
}
|
时间复杂度:$O(n^2)$
空间复杂度:$O(n^2)$
题目描述:
给定你一个长度为 n 的整数数列。
请你使用快速排序对这个数列按照从小到大进行排序。
并将排好序的数列按顺序输出。
输入格式:
输入共两行,第一行包含整数 n
第二行包含 n 个整数(所有整数均在 $1$∼$10^9$ 范围内),表示整个数列。
输出格式:
输出共一行,包含 n个整数,表示排好序的数列。
输入样例:
输出样例:
数据范围:
$$
1 \leq n \leq 100000
$$
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
#include <iostream>
using namespace std;
const int N = 100010;
int n,q[N];
void quick_sort(int q[],int l,int r)
{
if (l >= r) return;
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while (i < j)
{
do i++; while (q[i] < x);
do j--; while (q[j] > x);
if (i < j) swap(q[i],q[j]);
}
quick_sort(q,l,j);
quick_sort(q,j+1,r);
}
int main()
{
scanf("%d",&n);
for (int i = 0; i < n; i++) scanf("%d",&q[i]);
quick_sort(q,0,n-1);
for (int i = 0; i < n; i++) printf("%d ",q[i]);
return 0;
}
|